Ecuaciones de la recta.
Concepto de recta: aunque matemáticamente no existe una definición de recta, una idea conceptual de recta es “un conjunto de puntos sucesivos sobre una misma línea, que se extiende al infinito por ambos lados”.
La ecuación de una recta queda determinada si se conoce:
\(1.\) Dos puntos por donde pasa.
\(2.\) Un punto por donde pasa y su pendiente.
Definición de pendiente de una recta no vertical
Sea la recta \(y=mx+n\) una recta no vertical cualquiera, la pendiente \(m\) de la recta, es la tangente de su ángulo de inclinación \(\theta\) (theta) con el eje horizontal, dada por:
Pendiente de una recta no vertical
$$m=\tan{θ} =\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}~~~~~\mathrm{donde}~~x_2≠x_1$$
Ejemplo 1. Determine la pendiente de la recta que pasa por los puntos \((2, 4)\) y \((6, 8).\)
Solución: comience por identificar los puntos \(P_1=(2, 4)=(x_1, y_1)\) y \(P_2=(6, 8)=(x_2, y_2)\) ahora determine la pendiente.
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{8-4}{6-2}=\frac44=1$$
Intercambie los puntos \(P_1\) y \(P_2\) y determine nuevamente la pendiente ¿Qué puede concluir del resultado?
Solución: aplicando la definición de pendiente,
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-8}{2-6}=\frac{4}{4}=1$$
Como se puede ver no importa que punto se elija como \((P_1)\) o \(P_2\) lo que importa es que \(x_1\) esté junto con \(y_1\) y \(x_2\) junto a \(y_2\).
Ejemplo 2. Determine el valor de \(x\) para que la pendiente entre los puntos \(\left(3,5\right)\) y \(\left(x,\ 7\right)\) sea 2.
$$m=\frac{y_2-y_1}{x_2-x_1}\ \ \Longrightarrow2=\frac{7-5}{x-3}\ \ \Longrightarrow\ 2\left(x-3\right)=2$$
$$2x-6=2\Longrightarrow x=\frac{2+6}{2}\Longleftrightarrow x=4~~~~~~~~~~~~~~~~~~~$$
Formas de las ecuaciones de una rectas.
Una recta puede tener tres orientaciones geométricas básicas, horizontal, vertical y oblicua, esto da origen a distintas formas analíticas para la ecuación de una recta. Según la inclinación de una recta su ecuación puede tomar una o más de las siguientes formas:
Ecuaciones de la recta
\begin{array}{l l} {\rm ~~~~~~~~~~~~~Forma}& {\rm Ecuación}\\ \hline {\rm Recta ~horizontal},~m=0& x=n\\ {\rm Recta~vertical}, m=∞~~ {\rm (indefinida)}& y=n\\ {\rm Pendiente~intercepto~pasa~por~}(0,n)&y=mx+n\\ {\rm Punto~pendiente~pasa~por~}(x_1,y_1)&y=m(x-x_1)+y_1\\ {\rm Forma~general,}~~m=-a/b&ax+by+c=0\end{array}
Ejemplo 3: Determine la ecuación de la recta que pasa por los puntos \((2, 3)\) y \((4,-2)\)
Solución: la ecuación buscada tiene la forma \(y=m(x-x_1)+y_1\) o la forma general (si se desea), se inicia por determinar la pendiente usando los dos puntos dados.
\begin{align}
&m=\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}\\
&m=\frac{-2-3}{4-2}⟹m=-\frac{5}{2}\end{align}
Usando ahora \(y=m(x-x_1)+y_1\) para \(m=-5⁄2\) y el punto \((2,3)\)
\begin{align}
&y=-\frac52(x-2)+3\\
&y=-\frac52x+5+3\\
&y=-\frac52x+8\end{align}
¿Qué pasaría si se utiliza \(m=-5⁄2\) y el punto \((4,-2)\)? El resultado no cambiaría, puede comprobarlo si lo desea.
Intersecciones.
Los puntos en que una recta interseca (corta) los ejes de abscisa y ordenada se llaman interceptos y se representan con los puntos \((a,0)\) para el eje de abscisa (eje horizontal) y \((0,n)\) para el eje de ordenada (eje vertical). Estos quedan determinados de manera simple al hacer \(x=0\) para la intercepción en ye, o \(y=0\) para la intercepción en \(x.\)
Ejemplo 4. Determine la ecuación de la recta que pasa por \((0,\ 6)\) y su pendiente \(m=2.\)
Solución: se tienen los elementos para la forma pendiente intercepto \(y=mx+n\) dado que \(\left(0,6\right)=\left(0,n\right)\) es intercepto en ye, de donde, \(y=2x+6.\) Si no se recuerda la forma pendiente intercepto, la forma \(y=m\left(x-x_1\right)+y_1\) siempre produce el resultado y puede usarse como sigue.
\(y=2\left(x-0\right)+6\Longrightarrow y=2x+6\)
Ejemplo 5. Determinar la ecuación de la recta con pendiente \(m=0\) y pasa por el punto \((4, 7).\)
Solución: para \(y=mx+n\) si \(m=0\) se tiene la recta horizontal \(y=n\). La recta horizontal que pasa por \((4, 7)\) es \(y=7\)
Aplicaciones de las rectas. Modelos lineales.
Los modelos lineales y las aplicaciones son estudiados al analizar las funciones, si desea verlos haga click en funciones lineales o afines para ver su uso en el contexto del diario vivir. En este momento el enfoque está centrado en el estudio analítico de las propiedades algebraicas de las expresiones de la recta.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Forma simétrica de la ecuación de la recta.
Para finalizar el análisis de las ecuaciones de una recta se tiene que la ecuación de una recta cuyos interceptos son los puntos \(\left(a,0\right)\) y \(\left(0,b\right)\) puede escribirse como:
Forma simétrica de la recta
$$\frac{x}{a}+\frac{y}{b}=1$$
Ejemplo. Determinar los puntos de intercepción con los ejes cartesianos y la forma simétrica de la recta \(5x+2y-16=0.\)
Solución 1: Determinando los interceptos primero.
Intercepto en \(x:\) hacer \(y=0\) en \(5x+2y-16=0.\)
\(5x-16=0\Longleftrightarrow x=16/5\) de donde se tiene el punto \(\left(16/5,\ 0\right)=\left(a,0\right)\)
Intercepto en \(y:\) hacer \(x=0\) en \(5x+2y-16=0.\)
\(2y-16=0\ \Longleftrightarrow y=8\) de donde se tiene el punto \(\left(0,\ 8\right)=\left(0,b\right)\)
y por tanto la expresión buscada es,
$$\frac{x}a+\frac{y}b=1\Longrightarrow \frac{x}{16/5}+\frac{y}8=1$$
Solución 2: Determinando los interceptos al final.
\begin{array}{l l}
5x+2y-16=0& {\rm Ecuación~ dada.}\\
5x+2y= 16 & {\rm Trasposición}\\
\frac{5x}{16}+\frac{2y}{16}=\frac{16}{16}& {\rm Dividiendo~ entre} \ 16\\
\frac{x}{16/5}+\frac{y}{16/2}=1& {\rm Reescribiendo}\\
\frac{x}{16/5}+\frac{y}{8}=1& {\rm Reescribiendo\ en\ forma\ simétrica.}\end{array}
Comparando ahora,
$$\frac{x}{16/5}+\frac{y}{8}=1\ {\rm con}\ \frac{x}{a}+\frac{y}{b}=1$$
los puntos de intersección son $$\left(a,0\right)=\left(16/5,\ 0\right)\ \ {\rm y}\ \ \left(0,b\right)=\left(0,8\right).$$
Ecuación de la recta por determinante.
Para finalizar el análisis de las ecuaciones de una recta se muestra como determinar la ecuación de una recta mediante el uso de determinantes de orden \(3\times3\).
Dados dos puntos cualesquiera \(A(x_1,y_1)\) y \(B(x_2,y_2)\) la ecuación de una recta que pasa por ellos puede escribirse mediante la resolución del determinante siguiente:
Multiplicando los elementos en las diagonales que indican las flechas (los productos azules conservan sus signos mientras que los productos rosas cambian de signo). $$x(y_1)1+y(1) x_2+1(x_1) y_2-1(y_1) x_2-x(1) y_2-y(x_1)1=0$$ \(3.\) Simplificar el resultado anterior para escribir una ecuación en la forma \(ax+by+c=0\) que es la ecuación de la recta buscada.
Ejemplo 3. Determinar la ecuación de la recta que pasa por los puntos \((2,3)\) y \((4,-2)\) usando determinantes, luego determinar la pendiente.
Simplificando se tiene \(5x+2y-16=0\) que es el resultado.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Rectas paralelas y perpendiculares.
En geometría plana se dice que dos o más rectas son paralelas cuándo estando en el mismo plano nunca se cruzan, mientras que dos rectas son perpendiculares (normales) cuando al intersecarse forman un ángulo recto. Sin embargo, la descripción analítica de estos conceptos es muy diferente, si se conocen las pendientes de dos rectas se puede establecer las condiciones de paralelismo y perpendicularidad entre ellas (si la hay), mediante la observación de los valores de sus pendientes como sigue.
Rectas paralelas y perpendiculares.
1. Dos o más rectas son paralelas, si y solo si, sus pendientes son iguales, esto es, \(L_1∥L_2⟺m_1=m_2\)
2. Dos rectas son perpendiculares (o normales), sí y solo si, el producto de sus pendientes es \(-1,\) esto es
\(L_1⊥L_2 ⟺m_1 m_2=-1\)
Ejemplo 1. Determinar la ecuación general de la recta que pasa por \((3, 4)\) y es paralela a \(7x-3y+13=0.\)
Solución: como la recta buscada es paralela a \(7x-3y+13=0\) sus pendientes son iguales, de donde
\(m_2=m=-a/b\Longrightarrow m=-7/3\)
Aplicando ahora la ecuación punto pendiente para \(m=7/3\) y el punto \((3,4).\)
\begin{align}
&y=\frac73(x-3)+4\\
&y=\frac73x-7+4\\
&y=\frac73x-3\\
&7x-3y-9=0\end{align}
Ejemplo 2. Determinar la ecuación de la recta normal a \(3x+4y-5=0\) en el punto \((1/2, 1/3).\)
Solución: como son normales \(L_1⊥L_2\) entonces \(m_1 m_2=-1,\) donde \(m_1=-a⁄b\) en \(ax+by+c=0.~ m_2\) es la pendiente de la recta normal que se debe determinar.
$$m_1 m_2=-1⟹m_2=-\frac{1}{m_1} ⟺m_2=\frac{-1}{-3⁄4}=\frac43$$
Aplique ahora la ecuación punto pendiente para \(m_2=4/3\) y el punto \((1/2, 1/3)\)
\begin{align}
&y=m(x-x_1)+y_1\\
&y=\frac43(x-\frac12)+1\\
&3y=4(x-\frac12)+3\\
&3y=4x-2 ⟹ 4x-3y-1=0\end{align}
es la recta buscada en su forma general.
Ángulo entre dos rectas.
El hecho de que dos rectas sean normales implica un ángulo de noventa grados entre ellas, sin embargo, el ángulo entre dos rectas puede ser cualquier ángulo como se verá a continuación.
Para determinar el ángulo entre dos retas se seguirá el convenio de que un ángulo es positivo si gira contrario al sentido de giro de las agujas del reloj y negativo si gira en el sentido de las agujas del reloj, la recta a partir del cual parte el ángulo es la recta inicial cuya pendiente es \(m_1\) y la recta a la cual se dirige es la recta final cuya pendiente es \(m_2\) de donde el ángulo formado por ellas está dado por,
Ángulo entre dos rectas
$$\theta=\tan^{-1}\frac{m_2-m_1}{1+m_2m_1}\mathrm{\ \ \ \ \ siempre\ que\ \ }m_2m_1\neq-1$$
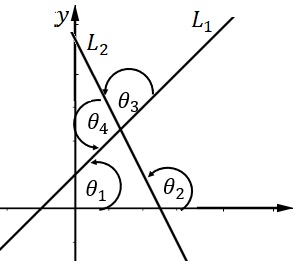Demostración: de la figura de la izquierda se desea demostrar que,
$$\theta_1=\tan^{-1}\frac{m_2-m_1}{1+m_2m_1}$$
partiendo de los ángulos, \(\alpha_1,\alpha_2\) que representan los ángulos entre las rectas \(L_1\) y \(L_2\) y el eje equis positivo, y los ángulos suplementarios \(\theta_1\) y \(\theta_2\) formados al intersecarse las rectas. Por geometría se sabe que los ángulos opuesto por el vértice son congruentes y que la medida de un ángulo exterior cualquiera es igual a la suma de los ángulos interiores no adyacentes, de donde \(\alpha_2=\alpha_1+\theta_1\) o de manera equivalente, \(\theta_1=\alpha_2-\alpha_1\) que al tomar tangente en ambos miembros es \(\tan{\theta_1}=\tan{\left(\alpha_2-\alpha_1\right)}.\) y de la trigonometría resulta:
$$\begin{array}{l l}
\tan{\theta_1}=\frac{\tan{\alpha_2}-\tan{\alpha_1}}{1+\tan{\alpha_2}\tan{\alpha_1}}&{\rm Por\ ser}\ \tan{\left(u-v\right)}=\frac{\tan{u}-\tan{v}}{1+\tan{u}\tan{v}}\\
\tan{\theta_1}=\frac{m_2-m_1}{1+m_2m_1}&{\rm Por\ ser}\ m=\tan{\alpha}\\
\theta_1=\tan^{-1}\frac{m_2-m_1}{1+m_2m_1}&{\rm Tomando}\ \tan^{-1}\ {\rm en\ ambos\ lados.}\end{array}$$
Lo que queda demostrado (l.q.q.d.).
Note que si \(m_2m_1=-1\) la expresión no está definida por los que las rectas son perpendiculares \((\theta=90°)\) como ya se sabía.
Ejemplo. Determinar el ángulo de inclinación entre las rectas \(y=0\) y \(y=x.\)
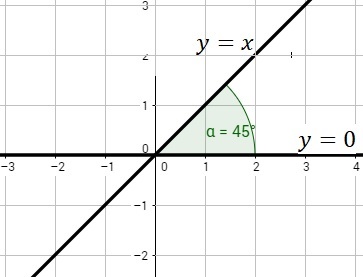Solución: aplicando la expresión
$$\theta=\tan^{-1}\frac{m_2-m_1}{1+m_2m_1}$$
para \(m_1=0\) (recta horizontal \(y=0\)) y \(m_2=1\) (recta inclinada \(y=x\)) se tiene,
$$\theta=\tan^{-1}\frac{1-0}{1+0}=45°$$
Para más contenidos y luego clic en la pestaña de ejercicios.
Una recta oblicua. Determine la ecuación de la recta que pasa por \((0,\ 6)\) y su pendiente \(m=2.\)
Una recta horizontal. Determinar la ecuación de la recta que pasa por el punto \((4,\ 7)\) y pendiente \(m=0\)
Una recta vertical. Determinar la ecuación de la recta que pasa por los puntos \((3,\ 7)\) y \((3,\ 11).\)
Una recta normal. Determine la ecuación general de la recta que es perpendicular \(4x-5y+12=0\) y pasa por el punto \((4,8).\)
Una recta normal. La recta que pasa por \((2, 4)\) y \((3,-2)\) es normal a la recta que pasa por \((4, 2)\) y \((x,1).\) Determinar el valor de \(x\) para que esto sea cierto.
Triángulo rectángulo. Empleando el concepto de pendiente, demuestre que \((6, 5), (-3, 0)\) y \((4, -2)\) son los vértices de un triángulo rectángulo.
Recta paralela. Determinar la ecuación de una recta que pasa por \((7, 5)\) y que es paralela a la recta \(5x\ -2y\ +15\ =0.\)
Condición para rectas paralelas. La recta que pasa por \((6,-4)\) y \((-3,2)\) es paralela a la que pasa por \((2,1)\) y \((0,y).\) Calcular el valor de \(y\).
Recta normal. Determinar la ecuación de una recta que es perpendicular a \(x-7y-11=0\) en su intersección con \(3x + 5y -7=0\)
Intersección de rectas: Encontrar el punto de intersección de la recta que pasa por \((2, -3)\) y \((-4, 6)\) con la recta que pasa por \((5, 3)\) y \((1, -1/3).\)
Determinando una contante. Determinar el valor de \(y\) si la distancia entre \((7, 1)\) y \((3, y)\) es \(5\)